| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- ac 5430번
- append
- 백준 1043번 거짓말 - java 분리 집합
- 프로그래머스 java
- replace()
- 프로그래머스 자바
- 백준 2467번 용액 자바 - 이분탐색
- map
- mysql hy000 에러
- 백준 1806번 부분합 java
- hash
- Stack
- Java
- 백준 2473번 세 용액 - java
- HashMap
- 백준 3190번
- StringTokenizer
- 백준 14938번 서강그라운드
- 백준 1197번 최소 스패닝 트리 - java
- 백준 1647번 도시 분할 계획 - java
- toUpperCase
- HashSet
- 최소 힙 1927
- StringBuilder
- 코틀린기초
- dp
- kotlin
- 18111번 마인크래프트 - java 구현
- 백준 1541
- 프로그래머스
- Today
- Total
말하는 컴공감자의 텃밭
백준 12865번 평범한 배낭 G5 - DP 본문
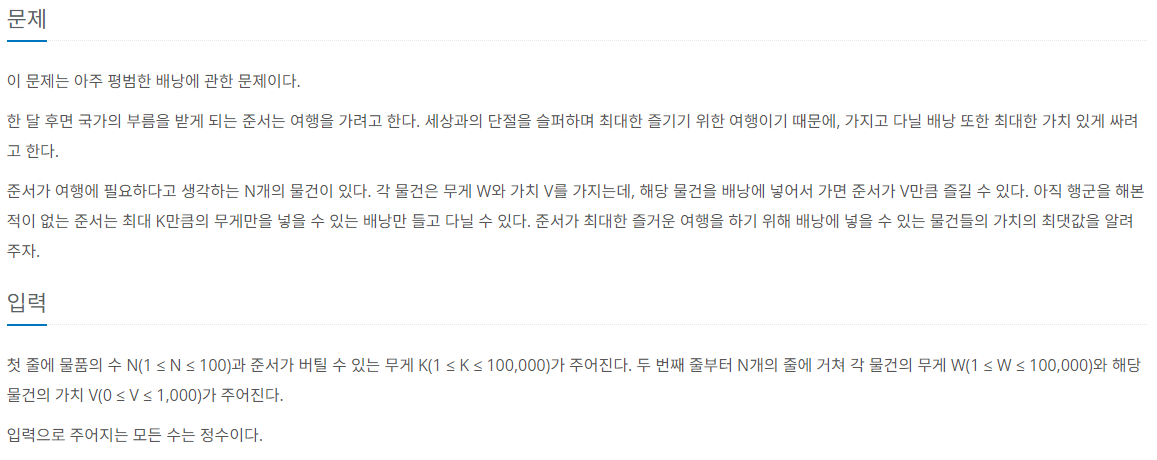
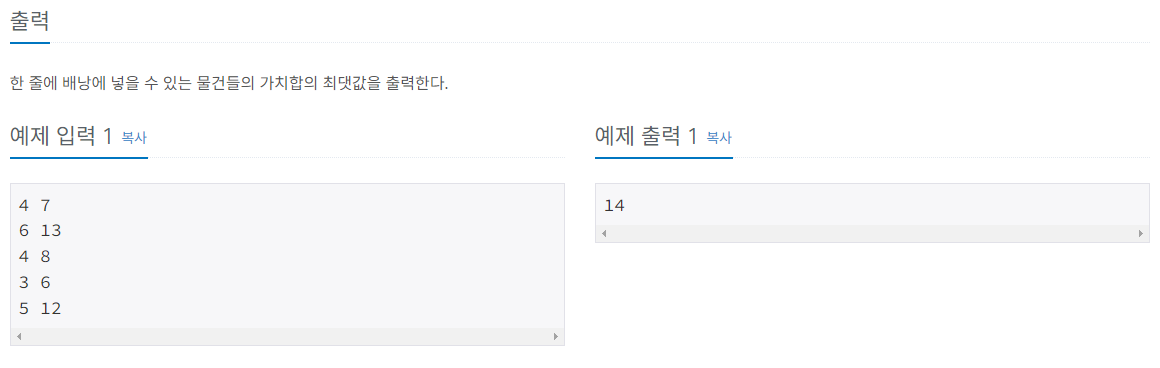
배낭 문제이다.
초등학교때 이런유형 문제 수학시간에 나왔던거 같아
하나하나 다 따지자니 중복이 많으므로 범위를 나눠서 큰 문제를 푸는 DP를 선택했다.
배낭의 무게에 여유가 있다면 해당 물건을 담고, 이후 가방에 더이상 넣을 수 없다면
배낭 안의 물건과 가치를 비교해서 넣어주면 되겠다.
2차원 배열로 가방의 순서대로 진행하되, 무게를 저장해줬다.
DP[ i ][ j ] 를 설명하면 i번째 물선 순서에 j의 무게를 담을 수 있는 가방 상황에서의 가치를 담고있다.
표로 정리해보면
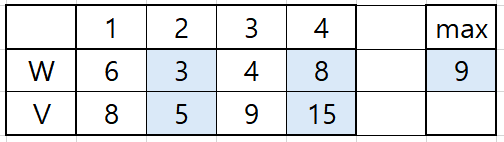
무게 최대는 9Kg라 가정. W는 무게, V는 가치이다.
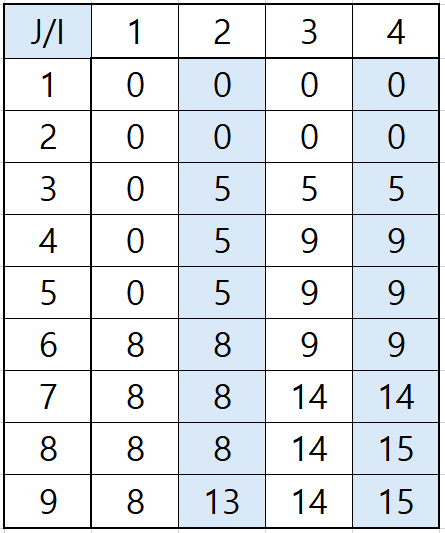
세로는 가방 무게인 J를 나타내고, 가로는 물건의 순서를 뜻한다. 초기에는 아무것도 들어있지 않으므로 0이다.
DP[1][6] 이후로는 무게 6의 가치8 물건을 넣을 수 있으므로
DP[1][6] = 8이되고 이후에 넣을 수 있는 물건이 없으므로 8이다.
DP[2][3] 부터는 무게3 가치5를 넣을 수 있으므로 5를 넣고, DP[2][6]은 기존 무게6 가치8이 더 높으므로 8을 넣어준다.
반복하면 DP[4][9] = 15로 가방에 담을 수 있는 최대 가치는 15이다.
결국 가방 수용량이 W[i]보다 같거나 크다면 기존 값과 V[i]를 더한 가치를 비교해서 큰 값을 갱신해준다.
만약 예시처럼 세번째 물건일때 7kg 가방이라면 (i = 3)(j = 7) DP[2][7]이랑 DP[2][7-4] + 9 랑 비교한다.
코드로 나타내면
if( j >= W[i]) DP[i][j] = Math.max(DP[i-1][j], DP[i-1][j-W[i]] + V[i]) 이 되겠다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | import java.util.*; import java.io.*; public class Main {// 12865번 평범한 배낭 // 배낭 문제, 다이나믹 프로그래밍 static int N, K; static int[][] dp; static int[] W,V; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine()); N = Integer.parseInt(st.nextToken()); K = Integer.parseInt(st.nextToken()); W = new int [N+1]; V = new int[N+1]; dp = new int[N + 1][K + 1]; for (int i = 1; i <= N; i++) { st = new StringTokenizer(br.readLine()); W[i] = Integer.parseInt(st.nextToken()); V[i] = Integer.parseInt(st.nextToken()); } // 가방에 물건을 넣을 수 있으면 넣는다. // 가방에 공간이 부족한경우, 안에 물건과 가치를 비교해서 넣는다. i = 가방번호, j = 무게 for(int i = 1; i<=N; i++) { for(int j = 1; j<=K; j++) { dp[i][j] = dp[i-1][j]; if(j >= W[i]) { // 가방의 크기를 나눠준다 생각. dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-W[i]] + V[i]); } } } System.out.println(dp[N][K]); } } | cs |
'알고리즘 > Backjoon - Java' 카테고리의 다른 글
| 백준 15721번 번데기 S5 - Brute force (0) | 2024.01.15 |
|---|---|
| 백준 1181번 단어정렬 S5 - Comparable 인터페이스 (1) | 2024.01.03 |
| 백준 3085번 사탕 게임 S2 - 브루트포스 (0) | 2023.12.14 |
| 백준 2579번 계단 오르기 S3 - DP (0) | 2023.12.12 |
| 백준 2636번 치즈 G4 - BFS (0) | 2023.12.03 |





