| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 백준 1806번 부분합 java
- 프로그래머스 java
- map
- replace()
- 백준 2473번 세 용액 - java
- 백준 1197번 최소 스패닝 트리 - java
- mysql hy000 에러
- 코틀린기초
- kotlin
- 백준 1043번 거짓말 - java 분리 집합
- toUpperCase
- StringTokenizer
- Java
- 백준 14938번 서강그라운드
- 백준 1647번 도시 분할 계획 - java
- HashMap
- append
- 최소 힙 1927
- HashSet
- hash
- ac 5430번
- 18111번 마인크래프트 - java 구현
- 백준 1541
- dp
- 백준 2467번 용액 자바 - 이분탐색
- Stack
- StringBuilder
- 프로그래머스
- 백준 3190번
- 프로그래머스 자바
- Today
- Total
말하는 컴공감자의 텃밭
백준 1010번 다리놓기 <S5> - DP, 조합 본문

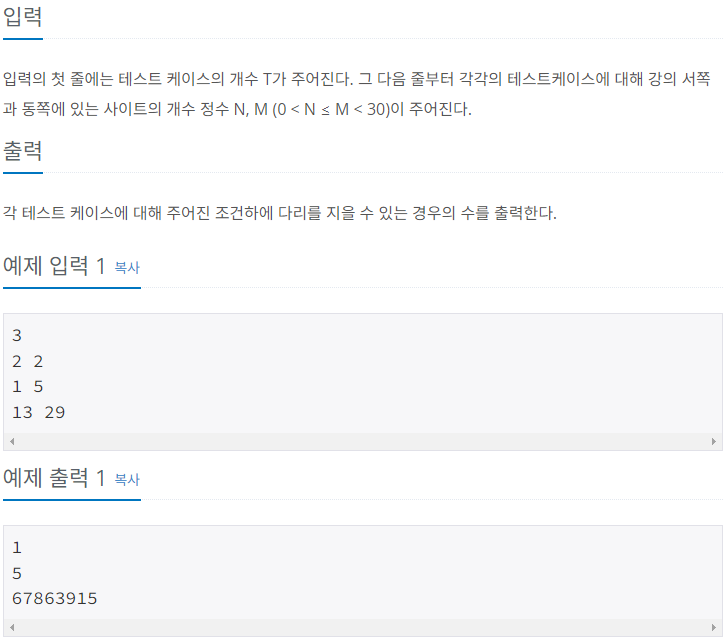
문제를 보자마자 조합? 이라고 생각했다.
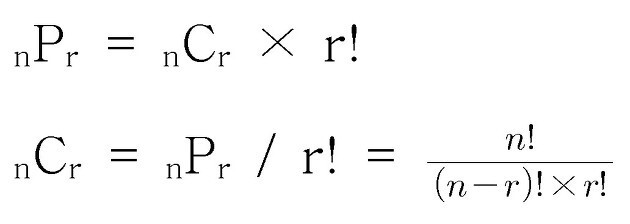
왼쪽 다리놓을 포인트와 오른쪽 다리 놓을 포인트가 주어지고, 그 사이에서 다리 를 연결할 수 있는 경우의 수 이다.
다리는 겹쳐지는것이 허용되지 않는다.
그럼 뭐 순서가 필요없는 조합이자나요~ 다리 1개만 놓을건데.
다만 수가 굉장히 크기 때문에 Big Integer을 사용하거나, 모든 경우의 수를 저장해놓고 더하는 방식으로 진행했다.
조합에서 파스칼 삼각형을 사용하여 점화식을 적용했다.

출처 : https://namu.wiki/w/%ED%8C%8C%EC%8A%A4%EC%B9%BC%EC%9D%98%20%EC%82%BC%EA%B0%81%ED%98%95
이항정리에서 사용된 이 파스칼의 삼각형의 특징은같은 층에서 옆에 수 끼리 더하면 밑의 값이 나오는 삼각형인데.
이를 잘보면 0C0 부터 5C0 의 값이다. 조합 특성 상 nCr + nCr+1 = n+1Cr+1 이기 때문이다. ( 기억 나시죠..? )
4C2 + 4C3 -> 5C3 이쟈나.
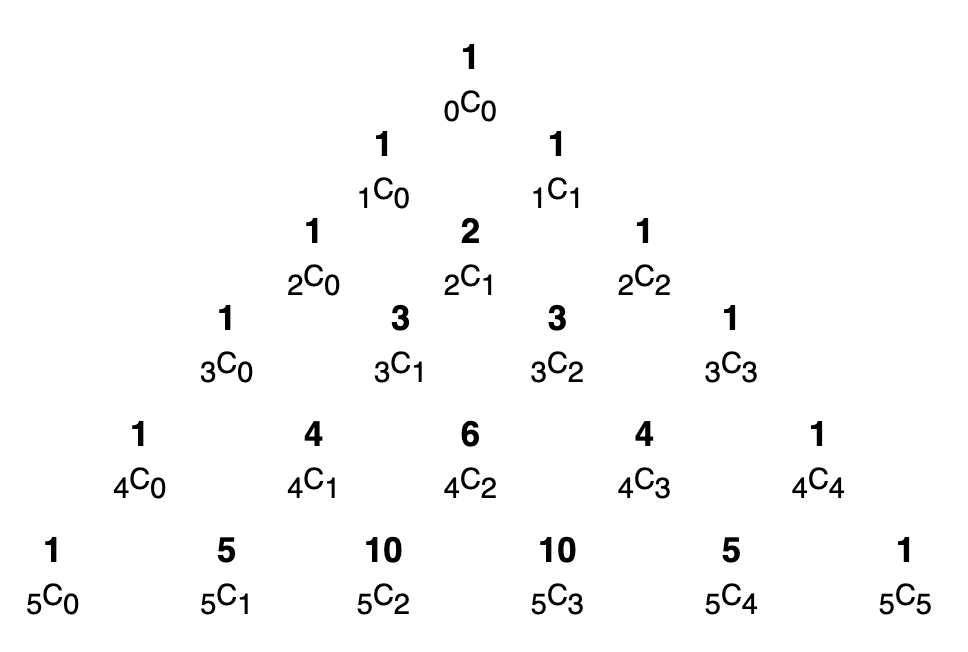
따라서 r c 조합을 계산해주고 r과 c가 같은건 모두 1로 dp[][]에 저장한 후
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 로 nCr + nCr+1 = n+1Cr+1 를 구현 해 주었습니다
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | import java.util.*; public class Main { // 1010번 다리 놓기 public static void main(String[] args) throws Exception { // 규칙이 조합과 동일. 1개만 놓기때문. // 다만 수가 너무 커지므로 연산을 기억해주는 dp[][] 생성. -> 재활용 위함 // 물론 BigInteger을 사용해서도 가능. int [][] dp = new int[31][31]; //input Scanner sc = new Scanner(System.in); int K = sc.nextInt(); for(int tc = 1; tc <= K; tc++) { int n = sc.nextInt(); // n = r int m = sc.nextInt(); // m = n int answer = 0; //logic //파스칼 활용. 2C1 + 2C2 = 3C2 //r이 1인경우와 n과 m이같은 경우. 무조건 1 for(int i = 1; i<31; i++) { dp[i][1] = i; for(int j = 2; j<31; j++) { if(i == j ) { dp[i][j] = 1; } } } for(int i = 2; i<31; i++) { // 2부터 진행해야함. for(int j = 2; j<31; j++) { dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; } } answer = dp[m][n]; // output System.out.println(answer); } } } | cs |
** 수정 : r과 c가 같은건 모두 1로 dp[][]에 저장한 후 로 1로 넣어준게 사실 상 코드 중복이고 읽기만 좋은용도라
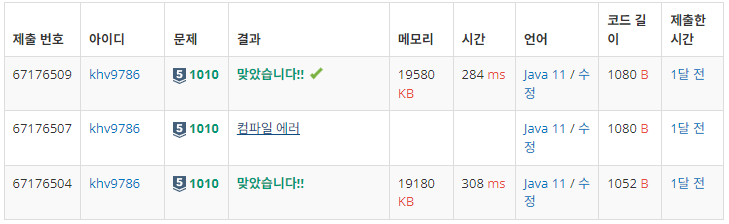
빼주는게 메모리적으로 효율이 좋았습니다~
'알고리즘 > Backjoon - Java' 카테고리의 다른 글
| 백준 26069번 붙임성 좋은 총총이 <S4> - Hash set (1) | 2023.10.27 |
|---|---|
| 백준 25192번 인사성 밝은 곰곰이 <S4> - Hash (0) | 2023.10.26 |
| 백준 1016 제곱 ㄴㄴ수 <G1> (1) | 2023.10.20 |
| 백준 1026번 보물 <S4> - 그리디 (0) | 2023.10.20 |
| 백준 13909번 창문 닫기 <S5> - 구현 (1) | 2023.10.20 |





