| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 백준 1541
- HashSet
- kotlin
- 프로그래머스 자바
- append
- StringTokenizer
- dp
- 백준 3190번
- hash
- toUpperCase
- 백준 1197번 최소 스패닝 트리 - java
- 백준 14938번 서강그라운드
- StringBuilder
- 백준 2467번 용액 자바 - 이분탐색
- ac 5430번
- 백준 1647번 도시 분할 계획 - java
- Stack
- 프로그래머스 java
- map
- HashMap
- 18111번 마인크래프트 - java 구현
- replace()
- 최소 힙 1927
- 백준 1043번 거짓말 - java 분리 집합
- Java
- 백준 2473번 세 용액 - java
- 프로그래머스
- 백준 1806번 부분합 java
- mysql hy000 에러
- 코틀린기초
- Today
- Total
말하는 컴공감자의 텃밭
백준 9465번 스티커 S1 - DP 본문

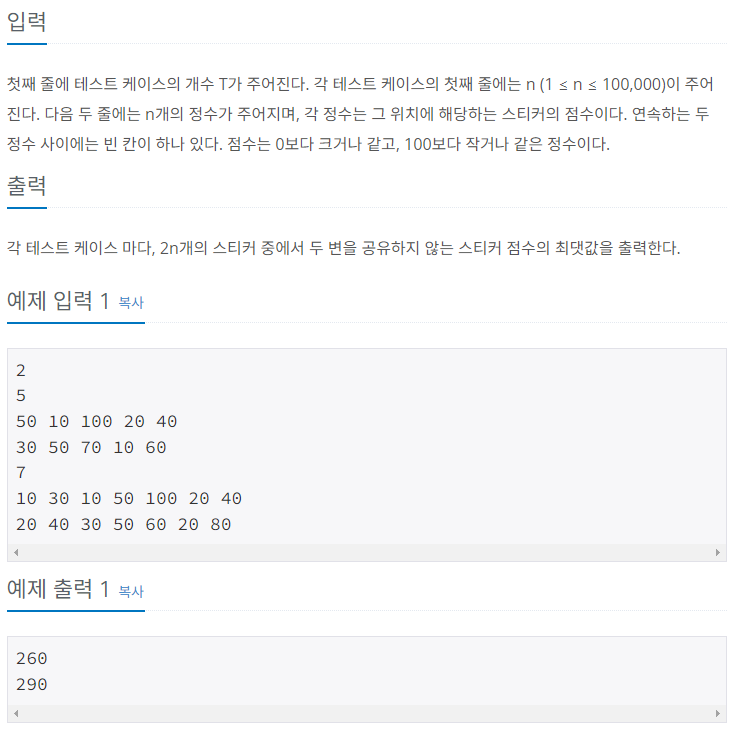
코테 준비할수록 DP 점화식을 찾거나 규칙 찾는거에 약한듯해서 DP위주로 준비하게 된다.
그래프는 이제 좀 감 잡았나 싶네 껄꼴껄~ 소주 땡긴다
문제를 읽고 가능한 수를 먼저 떠올리는 습관을 들였다.
문제를 보면 한 스티커를 선택하면 상하좌우 모두 사용이 불가능하다.
따라서 연속적으로 사용할 수 없고, 지그재그로 사용하면 가장 많은 수의 스티커를 붙일 수 있다.
하나의 경우가 더있는데
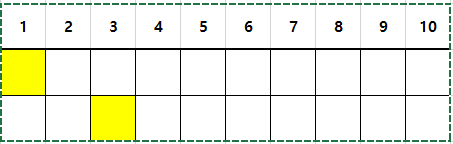
이런 경우도 존재했다.
어릴적 바둑배웠는데 '날일자' 日 생각나네
그러면 점화식을 세워준다. << 젤 어려운거
DP는 2차원으로 해주자, 위에 스티커를 떼는경우와 아래 스티커 떼는 경우가 존재하니.
초기에는 맨 왼쪽에 있는 스티커를 기준으로 최대값을 구해서 오류가 발생했었다.
시작이 위쪽인경우와 시작인 아래인 경우로 나눴는데 이상하게 답이 안나왔다..
// 맨 왼쪽을 상단을 선택하냐, 하단을 선택하냐
// 중간에 건너띄우는 방법도 존재함을 고려
dp[0][0] = arr[0][0];
dp[1][0] = arr[1][0];
dp[0][1] = dp[0][0] + arr[1][1];
dp[1][1] = dp[1][0] + arr[1][0];
// // 점화식
// dp[0][2] = Math.max(dp[0][1] + arr[0][2], dp[0][0] + arr[1][2]);
// dp[1][2] = Math.max(dp[1][1] + arr[1][2], dp[1][0] + arr[0][2]);
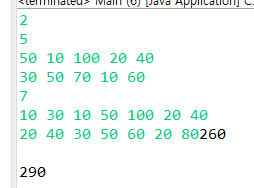
지금 생각해보면
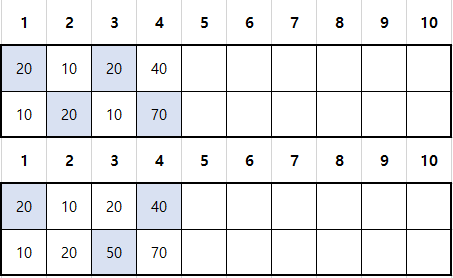
위 같은 상황이라면 DP[0][3] 은 70이지만 DP[0][4]는 130이 최대값이 된다.
결국 DP[0][4]에 DP[0][3]을 활용하지 못하게된다.
점화식에 오류가 있었고. 스티커를 뜯는 위치를 기준으로 바꿔주었다.
현재 뜯는 위치에서 전전과 전만 고려하면 되었다.
만약 내가 3번째 위쪽 스티커를 뗀다면 그 전 2번째 위쪽 스티커를 떼지 않았어야한다.
아래쪽이라면 그 전 아래쪽 스티커를 떼지 않았어야 한다.
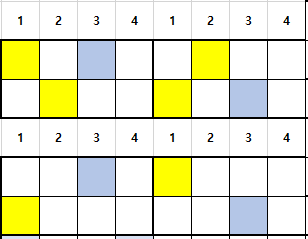
노란색은 떼진 스티커 위치이다. 파란색은 뜯을 위치이다.
3번째 위 스티커를 떼는 경우는 2가지가 존재하고,
3번째 아래 스티커를 떼는 경우 역시 2가지가 존재한다.
위 스티커 >> DP[0][3] = DP[1][0] + arr[0][3] 또는 DP[1][2] + arr[0][3]
아래 스티커 >> DP[1][3] = DP[0][0] + arr[1][3] 또는 DP[0][2] + arr[1][3]
으로 점화식을 세우면
for (int i = 2; i <= N; i++) {
dp[0][i] = Math.max(dp[1][i - 2], dp[1][i - 1]) + arr[0][i];
dp[1][i] = Math.max(dp[0][i - 2], dp[0][i - 1]) + arr[1][i];
}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | import java.util.*; public class Main { // 백준 11403번 경로 찾기 S1 // dp로 해결 N+1로 시작하자.. public static int N, answer; public static int[][] arr; public static int[][] dp; public static void main(String[] args) { Scanner sc = new Scanner(System.in); int T = sc.nextInt(); for (int tc = 1; tc <= T; tc++) { N = sc.nextInt(); arr = new int[2][N+1]; dp = new int[2][N+1]; for (int i = 0; i < 2; i++) { for (int j = 1; j <= N; j++) { arr[i][j] = sc.nextInt(); } } dp[0][1] = arr[0][1]; dp[1][1] = arr[1][1]; // // 점화식 // dp[0][2] = Math.max(dp[1][0],dp[1][1]) + arr[0][2]; // dp[1][2] = Math.max(dp[0][0],dp[0][1]) + arr[1][2]; for (int i = 2; i <= N; i++) { dp[0][i] = Math.max(dp[1][i - 2], dp[1][i - 1]) + arr[0][i]; dp[1][i] = Math.max(dp[0][i - 2], dp[0][i - 1]) + arr[1][i]; } int answer = Math.max(dp[0][N], dp[1][N]); System.out.println(answer); } } } | cs |
'알고리즘 > Backjoon - Java' 카테고리의 다른 글
| 백준 7579번 토마토 G5 - BFS (0) | 2023.11.18 |
|---|---|
| 백준 7576번 토마토 G5 - BFS (0) | 2023.11.17 |
| 백준 11403번 경로 찾기 S1 - 플로이드 위샬, BFS (0) | 2023.11.15 |
| 백준 골드 V 짜자작 (1) | 2023.11.14 |
| 백준 11866번 요세푸스 문제 0 <S5> - 구현 (0) | 2023.11.06 |





