| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- hash
- 백준 1043번 거짓말 - java 분리 집합
- Java
- 백준 2473번 세 용액 - java
- ac 5430번
- 프로그래머스 자바
- kotlin
- 18111번 마인크래프트 - java 구현
- 백준 1806번 부분합 java
- append
- Stack
- HashMap
- mysql hy000 에러
- 프로그래머스 java
- toUpperCase
- 백준 3190번
- dp
- StringTokenizer
- HashSet
- 백준 1647번 도시 분할 계획 - java
- 백준 2467번 용액 자바 - 이분탐색
- 최소 힙 1927
- 백준 1197번 최소 스패닝 트리 - java
- replace()
- 백준 14938번 서강그라운드
- 프로그래머스
- StringBuilder
- 코틀린기초
- map
- 백준 1541
- Today
- Total
말하는 컴공감자의 텃밭
백준 1647번 도시 분할 계획 - Java 최소 스패닝 트리 본문
도시 분할 계획

마을에는 경로가 존재하고, 분리해서 이 경로를 없애면서 유지비용을 최대한 줄이는 문제다.
마을 내부에서 서로 다른 집을 방문할 수 있어야하고, 마을이 분리됐다면 분리된 마을끼리는 연결되지 않아도 된다.
이게 말로만 풀어쓰니까 이게 무슨..? 싶은데 그림으로 정리하면 편하다.

파란 부분을 A마을, 붉은 부분을 B마을이라고 하자,
A 마을끼리 모두 연결되어 있고, B 마을끼리 모두 연결되어 있다.
A와 B 마을 사이에 연결되는 부분이 오늘 문제의 포인트다.
분할되는 부분이기 때문에 유지비가 들지 않는다.
그림을 다시보면 모든 점이 연결된 그래프고, 우리는 유지비를 최소한으로 유지하고 싶으므로
많은 경로가 존재한다면 그 중 유지비가 적은 값으로 연결을 시켜야 할것이다.
결국 이건 학부때 배웠던 최소 스패닝 트리(최소 신장 트리) 문제였다.
개념적으로만 이해했었는데 꼴꼴,,, 이제와서야 구현하고 있다니
일단 최소 스패닝트리는
주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
예제를 그림으로 그려서 풀어보자


각각의 경로와 가중치를 표기했다.
먼저 최소 비용으로 구성한 연결 그래프, 최소 신장트리를 만들어야한다.
방문하지 않은 idx를 순회하여 우선순위 큐에 넣는다.
방문하지 않은곳이라면 큐에서 꺼내 연결하고, 유지비용에 더해 저장한다.
이후 모든점을 순회하여 연결하면 MST(Minimum Spanning Tree) 가 완성된다.
우리는 마을 분리를 통해 유지비용을 줄일것이기에 연결된 부분중 가장 비용이 높은 부분을
끊어 마을을 분리해주면 최소값이 나오게 된다.



먼저 1부터 시작하고 합은 0으로 시작한다.
이후 입력에서 주어진 간선으로 연결된 부분을 찾는다.
1에서 2,3,5,6 을 우선순위 큐에 넣는다. 우선순위 큐 ➡ [ 3(2), 6(2), 2(3), 5(5) ]
우선순위 큐 가장 앞인 3를 poll()하고 거리를 더한다. 합 : 2
3과 연결된 부분을 우선순위 큐에 넣는다.
3에서 2, 4, 7 을 우선순위 큐에 넣는다. 우선순위 큐 ➡ [ 2(1), 6(2), 2(3), 4(4), 5(5), 7(6) ]
가장 앞인 2를 poll() 하고 거리를 더한다. 합 : 3
2와 연결된 부분을 우선순위 큐에 넣는다.
2에서 5를 우선순위 큐에 넣는다. ( 1과 3은 연결되었기에 넘어간다 )
우선순위 큐 ➡ [ 6(2), 5(2), 2(3), 4(4), 5(5), 7(6) ]
가장 앞인 6을 poll() 하고 거리를 더한다. 합 : 5

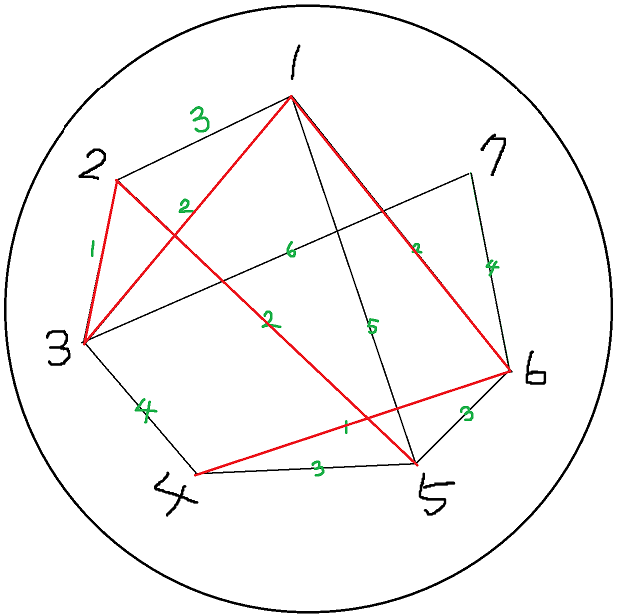

6과 연결된 부분을 우선순위 큐에 넣는다.
6에서 4,5,7을 우선순위 큐에 넣는다. 우선순위 큐 ➡ [ 4(1), 6(2), 5(2), 2(3), 5(3), 4(4), 7(4), 5(5), 7(6) ]
가장 앞인 4을 poll() 하고 거리를 더한다. 합 : 6
4와 연결된 부분을 우선순위 큐에 넣는다.
4에서 3,5를 우선순위 큐에 넣는다. 우선순위 큐 ➡ [ 6(2), 5(2), 2(3), 5(3), 5(3), 4(4), 7(4), 3(4), 5(5), 7(6) ]
순서대로 poll()하며 방문하지 않은 5까지 poll() 하고 거리를 더한다. 합 : 8
5와 연결된 부분을 우선순위 큐에 넣는다.
5에서 더이상 방문할 곳이 없다. 우선순위 큐 ➡ [ 2(3), 5(3), 5(3), 4(4), 7(4), 3(4), 5(5), 7(6) ]
순서대로 poll() 하며 방문하지 않은 7을 꺼낸다. 합 : 12
모든 점이 연결되었으므로 큐에 있는 값은 넘어간다.
이제 우리는 최소 신장트리를 완성했고, 이 간선중 가장 비용이 많이드는 부분을 잘라
마을을 나눠주면 최소비용이다. 예제에서는 7과 연결한 간선이(비용:4) max이므로 합에서 빼준값이 답이다.
합(12) - max(4) = 8

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 | import java.io.*; import java.util.*; public class Main { // 도시 분할 계획 static int N, M; static ArrayList<Node>[] list; static boolean[] visited; public static void main(String[] args) throws Exception { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine()); N = Integer.parseInt(st.nextToken()); M = Integer.parseInt(st.nextToken()); list = new ArrayList[N + 1]; for (int i = 1; i <= N; i++) { list[i] = new ArrayList<>(); } for (int i = 0; i < M; i++) { st = new StringTokenizer(br.readLine()); int s = Integer.parseInt(st.nextToken()); int e = Integer.parseInt(st.nextToken()); int cost = Integer.parseInt(st.nextToken()); list[s].add(new Node(e, cost)); list[e].add(new Node(s, cost)); } visited = new boolean[N + 1]; System.out.println(prim()); } public static int prim() { // 가장 유지비가 싼것부터 연결, 모두 연결되면 종료 PriorityQueue<Node> q = new PriorityQueue<>(); q.offer(new Node(1, 0)); int dist = 0; // 현재까지의 최소 경로의 간선 합을 저장한다. // 길 중 가장 큰 값을 마을을 분리할때 사용, ArrayList<Integer> checkedEdge = new ArrayList<>(); while (!q.isEmpty()) { Node current = q.poll(); if (!visited[current.idx]) { visited[current.idx] = true; checkedEdge.add(current.cost); dist += current.cost; for (Node next : list[current.idx]) { if (!visited[next.idx]) { q.offer(new Node(next.idx, next.cost)); } } } } // 가장 최대값을 찾아 합에서 제외하면 답. int max = checkedEdge.stream().max(Integer::compare).orElse(0); return dist - max; } public static class Node implements Comparable<Node> { int idx; int cost; public Node(int idx, int cost) { this.idx = idx; this.cost = cost; } @Override public int compareTo(Node n1) { return Integer.compare(this.cost, n1.cost); } } } | cs |
'알고리즘 > Backjoon - Java' 카테고리의 다른 글
| 백준 1197번 최소 스패닝 트리 - Java (0) | 2024.08.28 |
|---|---|
| 백준 18111번 마인크래프트 - Java 구현 (0) | 2024.08.27 |
| 백준 1806번 부분합 - Java 투 포인터 (0) | 2024.08.21 |
| 알고리즘 재활 15일차 - 11723, 1927, 5430번 (0) | 2024.08.19 |
| 알고리즘 재활치료 14일차 - 10816, 15666, 1504번 (0) | 2024.08.16 |





